PDF / June 3, 2024

precalculus questions and answers pdf

Precalculus questions and answers PDFs provide comprehensive resources for mastering essential math concepts. These documents offer detailed solutions, practice problems, and explanations, enhancing understanding and exam preparation effectively.

Overview of Precalculus and Its Importance

Precalculus is a foundational course that bridges algebra and calculus, focusing on functions, trigonometry, and analytic geometry. It equips students with essential skills for advanced mathematics and STEM fields. The subject emphasizes understanding function behavior, trigonometric identities, and conic sections, which are critical for solving real-world problems. Mastery of precalculus concepts enables students to approach calculus and higher-level math with confidence. PDF resources containing questions and answers provide structured practice, ensuring a thorough grasp of key topics and their applications. These materials are invaluable for self-study, exam preparation, and reinforcing problem-solving strategies.

Why Use PDF Resources for Precalculus Questions and Answers?

Precalculus questions and answers PDFs are highly recommended due to their convenience and accessibility. These documents provide a comprehensive collection of practice problems, solutions, and explanations, allowing students to refine their understanding of key concepts. PDF resources are portable, making them ideal for studying anywhere, and they often include both multiple-choice and open-response questions. This variety helps students prepare for different exam formats and reinforces their problem-solving skills. Additionally, PDFs are easily searchable and can be annotated, enhancing the learning experience; They serve as valuable tools for self-assessment and exam preparation, ensuring students are well-equipped to tackle precalculus challenges effectively.

Key Topics Covered in Precalculus Questions and Answers PDFs

Precalculus PDFs cover functions, trigonometry, conic sections, polynomials, and analytic geometry. These topics are essential for building a strong mathematical foundation.

Functions and Their Properties

<br />

Functions and their properties are fundamental in precalculus. PDF resources cover various types of functions, including linear, quadratic, polynomial, rational, exponential, and trigonometric functions. Key concepts such as domain, range, composition, and inverse functions are explored in depth. Questions and answers also address function transformations, such as shifts, reflections, and scaling, which are essential for understanding function behavior. Additionally, these resources provide practice problems on identifying odd and even functions, determining continuity, and analyzing asymptotes. Mastery of these topics is crucial for solving real-world problems and progressing to calculus. The detailed explanations and solutions in precalculus PDFs help students grasp these concepts effectively.

Trigonometry Basics

Trigonometry basics are extensively covered in precalculus PDFs, focusing on fundamental concepts such as angles, triangles, and trigonometric functions. Resources include problems on solving triangles, using the Law of Sines and Cosines, and understanding trigonometric identities. Key topics like the unit circle, periodicity, and graphing trigonometric functions are also emphasized. Questions address inverse trigonometric functions, Pythagorean identities, and applications in real-world scenarios. Additionally, PDFs provide practice in converting between radians and degrees, simplifying expressions, and solving trigonometric equations. These materials are designed to build a strong foundation for advanced math, offering clear explanations and step-by-step solutions to complex problems. Regular practice with these resources enhances problem-solving skills and conceptual clarity in trigonometry.

Conic Sections and Their Applications

Conic sections, including circles, ellipses, parabolas, and hyperbolas, are fundamental in precalculus. PDF resources provide detailed questions and answers on their standard equations, properties, and applications. Key topics include identifying conic sections from equations, graphing, and analyzing their geometric features. Applications in physics, engineering, and astronomy are highlighted, such as planetary orbits and projectile motion. Practice problems involve solving for foci, vertices, and asymptotes, as well as interpreting real-world scenarios. These resources also cover transformations and parametric equations of conic sections. By mastering these concepts, students gain a deeper understanding of their practical uses and improve their ability to solve complex problems in various fields. Regular practice with these materials enhances analytical and problem-solving skills effectively.

Polynomials and Rational Functions

Polynomials and rational functions are cornerstone topics in precalculus, essential for understanding advanced algebra and calculus. PDF resources offer extensive practice problems, solutions, and explanations for polynomial operations, including addition, subtraction, multiplication, and division. Key concepts such as factoring, roots, and graphing polynomials are thoroughly covered; Rational functions, involving ratios of polynomials, are explored through solving equations, simplifying expressions, and analyzing asymptotes. These materials also address real-world applications, such as modeling growth and optimization problems. By working through these questions and answers, students develop a strong foundation in manipulating and interpreting polynomial and rational functions, enhancing their problem-solving abilities and readiness for higher-level math.

Analytic geometry, a foundational topic in precalculus, involves the study of geometric properties using coordinate systems and algebraic methods. PDF resources provide detailed questions and answers on key concepts such as equations of lines, circles, and conic sections. Students learn to analyze and graph functions, interpret slopes and intercepts, and solve systems of equations geometrically. These materials also cover transformations, symmetry, and parametric equations, with step-by-step solutions to complex problems. Multiple-choice and free-response questions help reinforce understanding, while real-world applications illustrate the practical relevance of analytic geometry in fields like engineering and physics. Regular practice with these resources enhances spatial reasoning and problem-solving skills, preparing students for advanced math courses.

Types of Questions Found in Precalculus PDFs

Precalculus PDFs contain multiple-choice questions, short answers, and extended response problems. They include solving triangles, quadratic equations, and graphing functions, providing a comprehensive assessment of mathematical skills.

Multiple Choice Questions

Multiple choice questions in precalculus PDFs are designed to test quick recall and conceptual understanding. They cover topics like functions, trigonometry, and conic sections, offering options for answers. These questions are efficient for assessing knowledge retention and problem-solving speed. They often include algebraic manipulations, graph interpretations, and applications of theorems. The structured format helps students identify gaps in understanding. Correct answers are provided, enabling self-assessment and focused study. Explanations for each choice clarify common misconceptions, reinforcing learning. This format is ideal for exam preparation, mirroring standardized tests. Regular practice with multiple choice questions builds confidence and accuracy in tackling complex problems effectively.

Short Answer and Extended Response Questions

Short answer and extended response questions in precalculus PDFs require detailed explanations and step-by-step solutions. These questions assess in-depth understanding and the ability to articulate mathematical reasoning. They often involve solving complex problems, such as trigonometric equations, polynomial factoring, and analytic geometry applications. Extended response questions allow students to demonstrate critical thinking and problem-solving processes. Clear explanations and justifications are expected, fostering analytical skills. The answers provided in the PDFs include thorough solutions, enabling students to review and learn from their mistakes. This format is ideal for preparing for exams that require both accuracy and clear communication. Regular practice with these questions enhances the ability to tackle challenging problems confidently and systematically.

Problem-Solving Strategies in Precalculus

Effective strategies include identifying key concepts, applying appropriate formulas, and verifying solutions; Practice with diverse problems enhances critical thinking and mathematical reasoning, preparing for exams and advanced studies.

Understanding the Problem and Identifying Key Concepts

To solve precalculus problems effectively, it’s crucial to read questions carefully and identify key elements such as variables, constants, and required outcomes. Recognizing the type of problem, whether it involves functions, trigonometry, or algebra, helps in selecting the appropriate approach. For example, solving triangles requires understanding angles and sides, while quadratic equations involve identifying coefficients and applying formulas. Underlining or highlighting key terms can aid in focusing on essential information. Additionally, visual tools like graphs or diagrams can clarify relationships between variables. Practicing with diverse problems from PDF resources enhances the ability to recognize patterns and apply relevant concepts efficiently, ensuring a solid foundation for advanced math studies.

Applying Mathematical Formulas and Theorems

Successfully solving precalculus problems involves the precise application of mathematical formulas and theorems. For instance, when dealing with trigonometric identities, using the Pythagorean theorem or angle addition formulas is essential. In polynomial and rational functions, factoring and simplifying expressions are critical steps. PDF resources provide clear examples and step-by-step solutions, demonstrating how to apply these formulas correctly. Regular practice helps students memorize key theorems and understand when to use them. By mastering these applications, students can tackle complex problems with confidence, ensuring accurate and efficient solutions. This skill is vital for progressing in calculus and other advanced mathematical disciplines, as it builds a strong analytical foundation.

Checking Solutions for Accuracy

Verifying solutions is a crucial step in mastering precalculus concepts. PDF resources often include detailed explanations and answer keys, allowing students to cross-check their work. By comparing their solutions with provided answers, learners can identify errors and understand where they went wrong. This process reinforces understanding and builds problem-solving confidence. Additionally, many PDFs offer step-by-step breakdowns, enabling students to follow logical progressions and grasp underlying principles. Regularly reviewing and validating solutions helps solidify mathematical reasoning and ensures long-term retention of key concepts. This practice is indispensable for achieving academic success and excelling in standardized tests or exams.

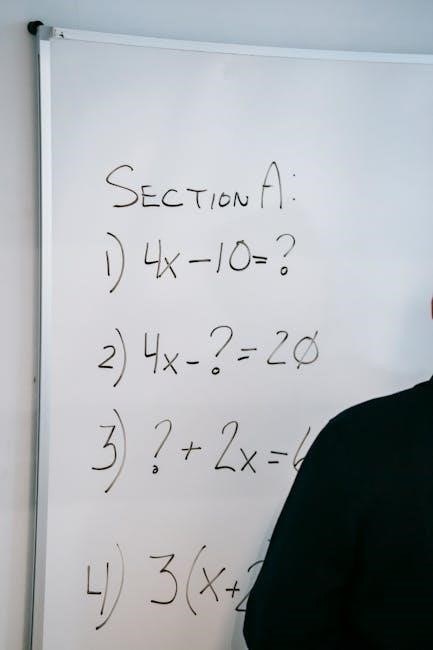
Benefits of Practicing with Precalculus PDFs

Practicing with precalculus PDFs enhances understanding, sharpens problem-solving skills, and prepares students for exams. These resources offer structured practice, improving conceptual clarity and boosting confidence in math abilities.

Improved Understanding of Complex Concepts

Precalculus questions and answers PDFs are invaluable for breaking down complex concepts into manageable parts. By practicing a wide range of problems, students gain a deeper grasp of functions, trigonometry, and polynomials. The structured format of these resources allows learners to tackle topics systematically, ensuring clarity and retention. Step-by-step solutions and detailed explanations help students understand how to approach challenging problems, fostering a solid foundation for advanced math. Regular practice with these materials also enhances analytical thinking and reduces confusion, making abstract ideas more accessible. This hands-on approach empowers students to master precalculus with confidence and precision, preparing them for future academic and professional challenges.

Enhanced Problem-Solving Skills

Engaging with precalculus questions and answers PDFs significantly enhances problem-solving abilities. These resources provide diverse problem types, from multiple-choice to extended response, challenging students to apply concepts creatively. By working through various scenarios, learners develop critical thinking and logical reasoning. The inclusion of step-by-step solutions allows students to analyze their approach, identify mistakes, and refine their strategies. Regular practice builds proficiency in breaking down complex problems into simpler, manageable parts. This skill is invaluable for tackling higher-level mathematics and real-world applications. Over time, students become adept at selecting appropriate methods and verifying solutions, ensuring accuracy and efficiency in their problem-solving processes.

Preparation for Standardized Tests and Exams

Precalculus questions and answers PDFs are invaluable for preparing students for standardized tests and exams. These resources often include practice questions that mirror the format and difficulty of actual test items, such as multiple-choice and short-answer problems. By working through these exercises, students gain familiarity with test structures and timing, reducing exam anxiety. The detailed solutions provided in the PDFs help learners identify areas of weakness and improve their test-taking strategies. Regular practice with these materials ensures a strong grasp of key concepts, enabling students to approach exams with confidence and readiness. This focused preparation is essential for achieving success in precalculus and beyond.